一张桌子上总共有 n 个硬币 栈 。每个栈有 正整数 个带面值的硬币。
每一次操作中,你可以从任意一个栈的 顶部 取出 1 个硬币,从栈中移除它,并放入你的钱包里。
给你一个列表 piles ,其中 piles[i] 是一个整数数组,分别表示第 i 个栈里 从顶到底 的硬币面值。同时给你一个正整数 k ,请你返回在 恰好 进行 k 次操作的前提下,你钱包里硬币面值之和 最大为多少 。
示例 1:
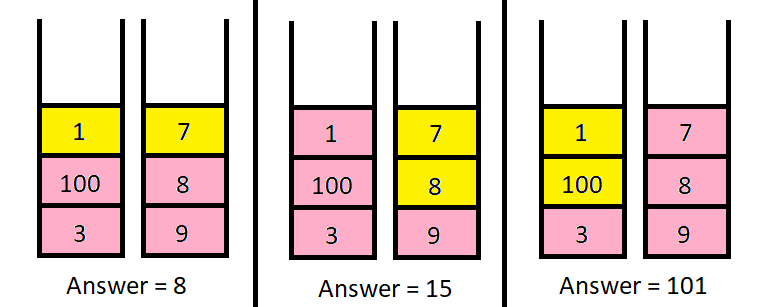
输入:piles = [[1,100,3],[7,8,9]], k = 2
输出:101
解释:
上图展示了几种选择 k 个硬币的不同方法。
我们可以得到的最大面值为 101 。思路
知道是dp,但是不知道怎么做😟。看了别人的题解才懵懵懂懂。思路是将问题转为0-1背包,每个栈可以选取体积为n的物品,体积即为前n位数,价值为前n位数值的和。最多可以装得下体积为k的背包,求装下物品价值的最大值。
代码
class Solution {
public int maxValueOfCoins(List<List<Integer>> piles, int k) {
int n=piles.size();
int[][] dp=new int[n+1][k+1];
//前i个栈
for (int i=1; i<=n; i++) {
//前i个栈取j个数的最大值
for (int j=0; j<=k; j++) {
int sum=0;
for (int m=0; m<=piles.get(i-1).size() && m<=j; m++) {
dp[i][j] = Math.max(dp[i][j], dp[i-1][j-m] + sum);
if (m <piles.get(i-1).size()) {
sum += piles.get(i-1).get(m);
}
}
}
}
return dp[n][k];
}
}